Steigung Durchfahrthöhe Gleisradien und Steigung Doppelgleisige Wendel Wendel als Oval Wendelberechnungsprogramm   Artikel-Download

Gleiswendeln erfreuen sich großer Beliebtheit bei Modellbahnern, gestatten sie doch die Überwindung beliebig großer Höhenunterschiede auf vergleichsweise kleinem Raum, siehe auch Meine Gleiswendel

Wie sich aber zeigen wird, kann der notwendige Raum nicht beliebig klein sein, wenn die Wendel im Fahrbetrieb Freude bereiten soll. Daher muss klar gesagt werden: Die häufig im Internet anzutreffenden Angebote von Fertig-Wendeln mit Steigungen von durchaus 4,5 % und mehr sind für Spur N problematisch und sollten nicht in Betracht gezogen werden. Wenn man einige Grundsätze beim Wendelbau beherzigt, ist das Ganze im Selbstbau mit zufrieden stellendem Ergebnis machbar. Im Folgenden stelle ich die Zusammenhänge für die Planung dar.

Steigung - Radius - Durchfahrthöhe

Dieses Trifolium ist stets untrennbar miteinander verbunden, d. h. es besteht zwischen diesen drei Größen eine unbestechliche mathematische Abhängigkeit. Der Radius bestimmt die Gleislänge pro Wendeldrehung und damit bei vorgegebener Durchfahrthöhe die Steigung. Schauen wir uns die drei Größen im Einzelnen an.

• Steigung

Wichtig ist es vor allem, die Steigung der Wendel festzulegen; denn die ist ausschlaggebend für einen späteren störungsfreien Betrieb. Was nützt eine sauber gebaute Wendel, wenn die Züge in einer zu starken Steigung schlappmachen? Hier sind also im Vorfeld unbedingt Versuche mit dem vorhandenen Rollmaterial angesagt, und nicht nur auf einer Geraden! Bei einer Wendel muss berücksichtigt werden, dass die Lok i.d.R. viele Meter Bogenfahrt zurücklegt, wobei an den Rädern erhöhte Reibung auftritt, was zusätzlich zur Anhängelast die Zug-Leistung vermindert. Diese Reibung nimmt mit kleiner werdendem Radius noch erheblich zu. Natürlich wird der Lokmotor auch stärker belastet, was naturgemäß seiner Lebensdauer abträglich ist. Weiterhin ist zu berücksichtigen, dass tendenziell bei neuen Loks im Vergleich zu älteren auch mit geringerem Gewicht und in der Regel nur 2 Haftreifen gerechnet werden muss. Es kann auch sein, dass eine Lok überhaupt keine Haftreifen aufweist. Das bedeutet, dass solche Loks schon auf Steigungen über 2,5 % möglicherweise Probleme bekommen.

Ein Beispiel:

Die wunderschöne BR 23 von Fleischmann ist mit nur 2 Haftreifen ausgestattet und hat Mühe, Steigungen über 2,5 % mit 5 bis 6 Reisezugwagen zu bewältigen. Sie beginnt dann zu schleudern. Meine alte BR 50 vom gleichen Hersteller hingegen zieht - mit 4 Haftreifen bestückt und schwerer als die BR 23 - ohne Probleme auch längere Züge auf Steigungen von 3,5 %.

 

Die Steigung eines Modell-Gleises wird im Allgemeinen in Prozent angegeben. Eine solche Zahl sagt aus, um wie viel Zentimeter ein Gleis auf einer Länge von 1 m steigt.

Die Länge eines gebogenen Gleises wird nach folgender Formel berechnet:

 

r x 2 x 3,14

Beispiel:

Die gestreckte Gleislänge eines Kreises aus Schienen mit Radius 350 mm (also einem Kreisdurchmesser von 700 mm) beträgt

 

350 x 2 x 3,14 = 2.198 mm

• Durchfahrt-Höhe

Die Trassen einer Wendel liegen logischerweise übereinander. Also muss der Zwischenraum zwischen zwei Trassen (eben die Durchfahrthöhe) festgelegt werden. Diese ist wiederum davon abhängig, ob mit E-Loks (wegen der Pantographen und ggf. montierter Oberleitung) oder nur mit Dampf- und Dieselloks gefahren wird.

Wer noch nicht weiß, ob er E-Loks einsetzen wird, sollte in jedem Fall die Wendel E-Lok-tauglich bauen. Nach NEM 201 werden drei Maße unterschieden, die das lichte Maß von Schienenoberkante bis Fahrdraht angeben.

H 1 Höchste Lage: H 2 Normallage: H 3 Tiefste Lage:

40 mm 38 mm 34 mm

 

Ferner müssen berücksichtigt werden

• Höhe der verwendeten Schienen
• Trassenstärke
• Höhe der verwendeten Geräuschdämmung (Kork, Resorb o.ä.)
• Platzbedarf der Fahrdraht-Aufhängung
• Sonstiges Montagematerial, das in den lichten Raum hineinragt (z.B. Trassen-Verschraubungen)
•  

Beispiel:

 

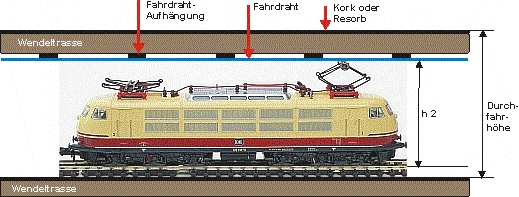Schienenhöhe: Maß h2: Fahrdrahtstärke: Fahrdrahtaufhängung: Trassenbrettstärke: Kork/Resorb: Durchfahrthöhe:

3 mm 38 mm 1 mm 3 mm 6 mm 3 mm 54 mm

(Genauer: Höhendifferenz zwischen zwei übereinander liegenden Wendeltrassen)

Die Schienenhöhe von 3mm gilt für Peco-Gleise (Code 55). Fleischmann-Gleise haben incl. ihres angespritzten Schotterbettes eine Höhe von 4 mm.

• Gleis-Radien und Steigung

Kommen wir nun zur häufig diskutierten Frage: Welche Radien sollte die Wendel aufweisen? Diese Frage ist natürlich von Bedeutung, da viele Modellbahner nur über beschränkten Platz verfügen und darum auf möglichst kleinem Raum "die Kurve kriegen" müssen. Hier muss man sich aber die noch aus der Schule bekannten geometrischen Gesetzmäßigkeiten klarmachen: Es besteht eine Abhängigkeit zwischen Radius, Steigung und der Durchfahrt-Höhe (Distanz zwischen den Trassen).

Wie man sehen kann, ist die Durchfahrt-Höhe, die man anhand seiner eigenen Gegebenheiten nach obigem Schema zuvor ermittelt hat, für die weiteren Berechnungen fest vorgegeben. Daraus folgt, dass die Steigung abhängig ist vom gewählten Radius der Schienen; denn je größer der Radius gewählt wird, umso länger wird das Gleis pro Wendelumdrehung, und umso geringer fällt die Steigung aus. Anders ausgedrückt: Da die Durchfahrthöhe nur in ganz engen Grenzen beeinflussbar ist, hängt die Steigung vom verfügbaren Platz für eine Wendel ab. Wer also feststellen muss, dass seine räumlichen Gegebenheiten nur Steigungen von 4 % oder gar noch stärker zulassen, der sollte lieber über andere Möglichkeiten, den Höhenunterschied zu überwinden, nachdenken. Es ist allemal besser, seinen Gleisplan dem technisch Machbaren anzupassen als eine Traumanlage zu verwirklichen, die sich später zum Albtraum entwickelt.

Die Berechnung der Steigung in Abhängigkeit von Radius und Durchfahrthöhe ergibt sich nach folgenden Formeln:

                        

Dieser Zusammenhang wird aus folgender Tabelle deutlich (mit zwei alternativen Durchfahrthöhen):

 

Radius in mm	Gleislänge pro Kreis in mm	Durchfahrt- Höhe1 in mm	Steigung 1 in %	Durchfahrt- Höhe2 in mm	Steigung 2 in %
192,0	1.206	54	4,5	58	4,8
228,2	1.433	54	3,8	58	4,0
295,4	1.855	54	2,9	58	3,1
329,0	2.066	54	2,6	58	2,8
362,6	2.277	54	2,4	58	2,6
396,4	2.489	54	2,2	58	2,3
430,0	2.700	54	2,0	58	2,2
480,0	3.014	54	1,8	65	2,2
492,6	3.094	54	1,8	65	2,1
526,2	3.305	60	1,8	70	2,1
600,0	3.768	60	1,6	75	2,0
700,0	4.396	65	1,5	90	2,0
800,0	5.024	65	1,3	100	2,0

Es ist ohne Weiteres erkennbar, dass die Fleischmann-Radien 3 und 4 (396,4 mm und 430 mm) selbst bei einer Durchfahrthöhe von 58 mm noch zu einer akzeptablen Steigung führen. Solange die Steigung zwischen   2 % bis 3 % liegt, sollte man einer größeren Durchfahrthöhe den Vorzug geben, sofern der Fahrzeug-Test positiv verlief. Denn man benötigt, wie man sieht, mit größer werdendem Radius zunehmend mehr Flexgleis, und der Bedarf daran steigt naturgemäß mit der Anzahl der Wendel-Windungen. Im Übrigen ist natürlich auch daran zu denken, dass die eigene Hand für Rettungsaktionen (die hoffentlich selten notwendig werden) zwischen die Trassen passen sollte.

Ein wichtiger Hinweis:

Wie bereits weiter oben erwähnt, wird die Leistung einer Lok in kleinen Gleisradien spürbar beeinträchtigt. Das geht soweit, dass manche Loks mit längerem Radstand (vor allem größere Dampfloks, deren Treibräder, im Gegensatz zu Drehgestellloks, starr gelagert sind) regelrecht "klemmen" und dann stehenbleiben. Manche Hersteller empfehlen für bestimmte Loks Mindestradien, und diese Empfehlungen sollte man tunlichst beachten. Darüber hinaus gilt eine grundsätzliche Empfehlung für N-Bahner: Kein Radius unter 300 mm, auch dort nicht, wo man es nicht sieht! Eigentlich trivial, aber immer wieder sträflich unbeachtet : Insbesondere die nicht einsehbahren Bereiche sind meistens auch die am schwersten zugänglichen. Nicht nur, dass die Behebung von Störungen an solchen Stellen (insbesondere in Wendeln) entsprechend fummelig ist; auch eine Korrektur der Gleisradien, die man später Einsicht folgend hier vornehmen möchte, ist fast immer unmöglich, oder geht mit einiger Zerstörung vorhergegangener Arbeit einher.

• Doppelgleisige Wendel

Bei Bau einer doppelgleisigen Wendel muss bedacht werden, dass der Radius des Innengleises die Steigung vorgibt. Beim äußeren Kreis ist die Steigung dann immer etwas schwächer. Wer es vom Gleisplan her hinbekommt, kann auch vor Ein- und Ausfahrt in die Wendel einen Gleiswechsel vornehmen, so dass immer auf dem größeren Radius bergauf gefahren wird. Bitte daran denken: Der Abstand beider Gleise (gemessen von Gleismitte zu Gleismitte) sollte ca. 34 mm betragen, damit sich im Begegnungsverkehr keine Berührung durch im Bogen ausschwenkende Fahrzeuge ergeben. Der Abstand kann mit größer werdenden Radien vermindert werden. So reichen bei Radien ab 370 mm auch 30 mm Gleismittenabstand aus. Im Zweifel sollte das zuvor auf zwei fliegend im gewählten Radius aufgebauten Parallelgleisen getestet werden (einfach zwei Flexgleise biegen und temporär mit ein paar Gleisnägelchen befestigen).

• Wendel als Oval

Es empfiehlt sich durchaus, seine Wendel als Oval zu bauen. Das hat drei Vorteile:

• Durch die in jede Wendel-Windung eingebauten geraden Gleisstücke werden die Loks kurzzeitig von ihrer "anstrengenden" Bogenfahrt entlastet.
• Es besteht in den Geraden die Möglichkeit, Eingleiser einzubauen, die dafür sorgen, dass (hoffentlich seltene) Entgleisungen während der Wendelfahrt nicht zu umständlichem Gefummele führen. Es ist nicht vergnügungssteuerpflichtig, einen festgekuppelten Ganzzug aus der Wendel zu fischen. Und manuelles Eingleisen in einer Wendel ist bei Loks und Wagen mit Drehgestellen fast nie möglich.
• Die geraden Gleisstücke bringen einen Längengewinn, was wiederum eine Reduzierung der Steigung bedeutet. Andersherum: Wer Platzprobleme in der Breite nicht aber in der Länge hat, kann auf diese Weise den Radius ein wenig reduzieren. Aber wirklich nur ein wenig!

 

• Programm zur Wendel-Berechnung

Auf seiner website www.n-modellbahn.de hat Joerg Kiessling einen beachtenswerten, reich bebilderten workshop zum Wendelbau veröffentlicht. Dazu steht auch ein kleines Excel-Programm zur einfachen Berechnung von Wendeln zum download zur Verfügung. Mit diesem Programm variiert man die Ausgangswerte einer geplanten Wendel (auch für Ovale möglich) so lange, bis das angezeigte Ergebnis für die eigenen Belange passt. Vor allem ist interessant, dass auch gleich eine Liste mit Höhenangaben für die einzelnen Trassenstützpunkte ausgegeben wird. Das ist beim Bau sehr hilfreich.

 

Abb. screenshot vom Wendelrechner